The Slantlet Transform
Abstract
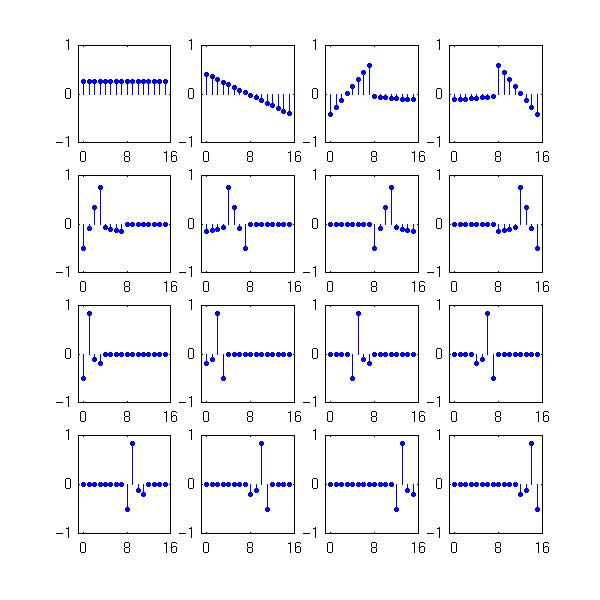
The discrete wavelet transform is usually carried out by filter bank iteration, however, for a fixed number of zero moments, this does not yield a discrete-time basis that is optimal with respect to time-localization. This paper discusses the implementation and properties of an orthogonal DWT, with two zero moments and with improved time-localization. The basis is not based on filter bank iteration, instead different filters are used for each scale. For coarse scales, the support of the discrete-time basis functions approaches 2/3 that of the corresponding functions obtained by filter bank iteration. This basis, a special case of a class of bases described by Alpert, retains the octave-band characteristic and is piecewise linear (but discontinuous). Closed form expressions for the filters are given, an efficient implementation of the transform is described, and improvement in a denoising example is shown. This basis, being piecewise linear, is reminiscent of the slant transform, to which it is compared.
I. W. Selesnick, The slantlet transform, IEEE Trans on Signal Processing, vol 47, no 5, pp 1304-1313, May 1999.
4 page conf. paper: The Slantlet Transform, Proceedings of the IEEE-SP Int. Symp. on Time-Frequency and Time-Scale Analysis , pages 53-56, Pittsburgh, October 6-9, 1998. postscript (205KB) or compressed postscript (45KB) file.
This work was carried out at the Lehrstuhl für Nachrichtentechnik, Universität Erlangen-Nürnberg, where it was supported by the Alexander von Humboldt Foundation.
Matlab code for the Slantlet transform
Download Slantlet Matlab Software (zip file, 55KB)
16-point slantlet basis:
Go to my home page.