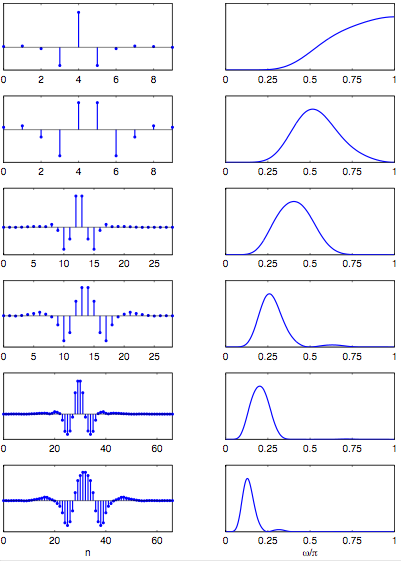
Examples
Tight frame with 3 vanishing moments
The wavelets of this example, from the paper, have 3 vanishing moments each.
The lowpass filter h0 and the bandpass filter h1 each have length 7, while
the highpass filter h2 has length 6.
The output of the lowpass and bandpass filters are both downsampled by 2,
while the output of the highpass filter is undecimated.
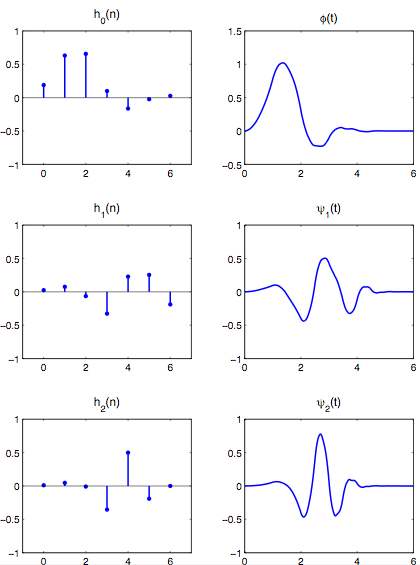
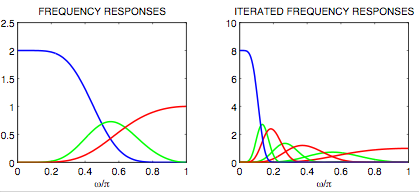
The coefficients of the filters are given in the table:
H0 - LOWPASS H1 - BANDPASS H2 - HIGHPASS 0.18960490937948 0.02575256366504 0.01016795615778 0.63145051212171 0.07546399806612 0.04675038012039 0.65550551835710 -0.06433334141293 -0.00917258487191 0.09961513980086 -0.32770469142887 -0.35466408768443 -0.16375621021508 0.22818568712737 0.49900462871412 -0.02395887073603 0.25224069336275 -0.19208629243595 0.02575256366504 -0.18960490937948 0
Tight frame with 4 vanishing moments
The wavelets of this example, from the paper, have 4 vanishing moments each.
The lowpass filter h0 and the bandpass filter h1 each have length 9, while
the highpass filter h2 has length 8.
The output of the lowpass and bandpass filters are both downsampled by 2,
while the output of the highpass filter is undecimated.
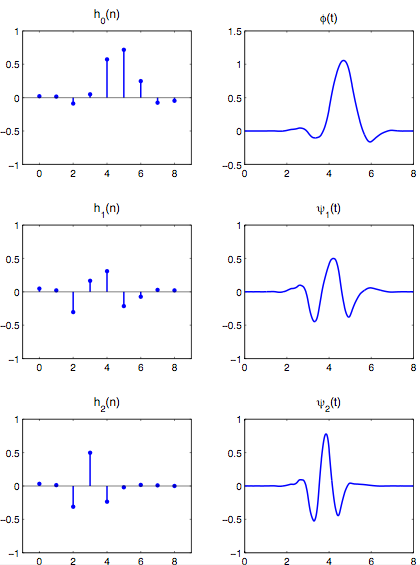
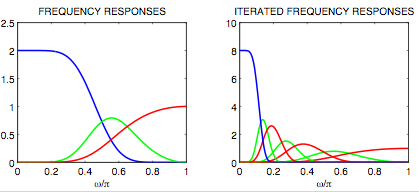
The coefficients of the filters are given in the table:
H0 - LOWPASS H1 - BANDPASS H2 - HIGHPASS 0.02203332757369 0.04847725477700 0.03129413583148 0.01538152261600 0.01999145194892 0.01324839800586 -0.08816908424543 -0.30453002403332 -0.31155229283304 0.05112094983499 0.16547892393019 0.49759432664884 0.57416137425815 0.30888491601268 -0.23511709248403 0.71756736634064 -0.21415550841048 -0.02059457665961 0.24755841837714 -0.07486547433005 0.01537524948558 -0.07696305760509 0.02868513253138 0.00975185200491 -0.04847725477700 0.02203332757369 0
Non-tight symmetric frame with 4 vanishing moments
This system is somewhat similar to the biorthogonal Daubechies 9/7 symmetric system - each wavelet has 4 vanishing moments, and the system is derived from the symmetric factorization of the symmetric polynomial from which the tight frame is derived. Like the 9/7 system, the synthesis wavelets are smoother than the analysis wavelets.
Analysis system
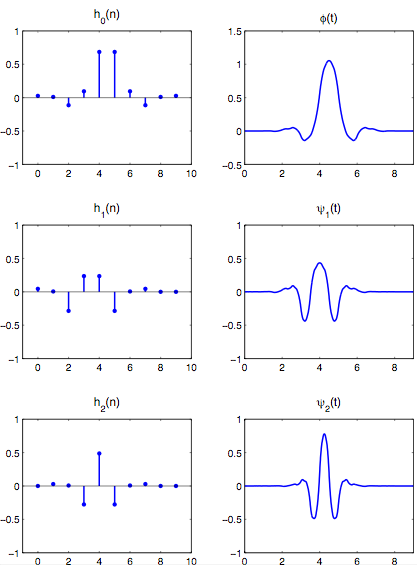
H0 - LOWPASS H1 - BANDPASS H2 - HIGHPASS 0.02722186296669 0.04488939651608 0 0.01121654966880 0.00567077289237 0.02767057807905 -0.11270921793626 -0.28634869777356 0.00715884384190 0.09607810395615 0.23578852836512 -0.27767057807905 0.68529948253117 0.23578852836512 0.48568231231620 0.68529948253117 -0.28634869777356 -0.27767057807905 0.09607810395615 0.00567077289237 0.00715884384190 -0.11270921793626 0.04488939651608 0.02767057807905 0.01121654966880 0 0 0.02722186296669 0 0
Synthesis system
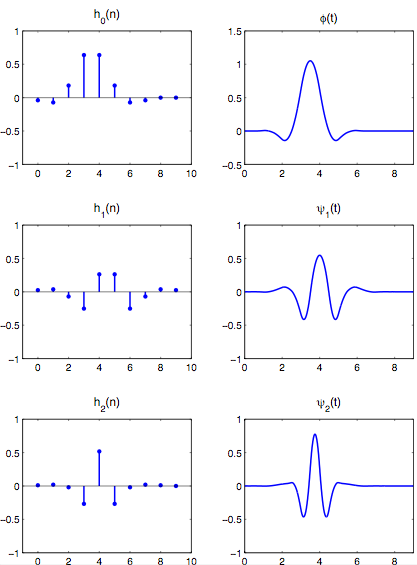
H0 - LOWPASS H1 - BANDPASS H2 - HIGHPASS
-0.03923740398231 0.02379437723099 0.01102889070037
-0.07351803812277 0.03778447272064 0.01920442192095
0.18173346513849 -0.07053788812010 -0.02002440664339
0.63812875815314 -0.25303694427344 -0.26920442192095
0.63812875815314 0.26199598244191 0.51799103188604
0.18173346513849 0.26199598244191 -0.26920442192095
-0.07351803812277 -0.25303694427344 -0.02002440664339
-0.03923740398231 -0.07053788812010 0.01920442192095
0 0.03778447272064 0.01102889070037
0 0.02379437723099 0
Iterated filters [Synthesis system]: