I. W. Selesnick and P.-Y. Chen, 'Total Variation Denoising with Overlapping Group Sparsity', IEEE Int. Conf. Acoust., Speech, Signal Processing (ICASSP). May, 2013.
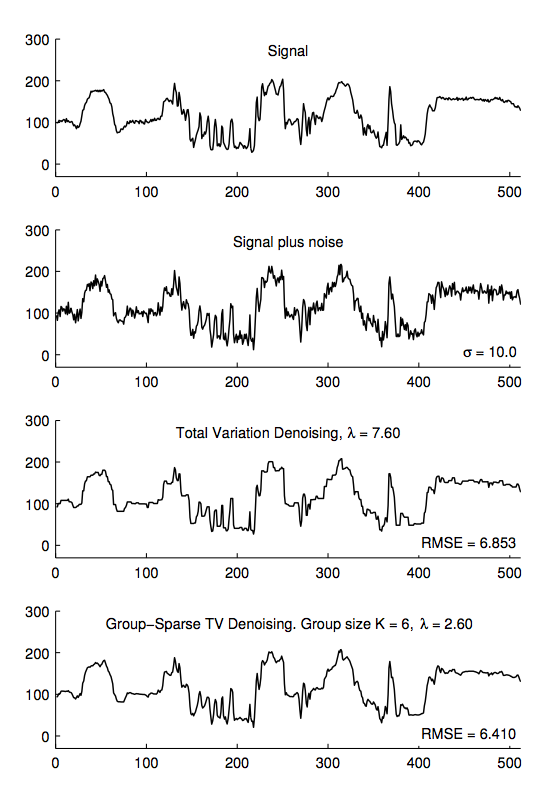
Abstract: This paper describes an extension to total variation denoising wherein it is assumed the first-order difference function of the unknown signal is not only sparse, but also that large values of the first-order difference function do not generally occur in isolation. This approach is designed to alleviate the staircase artifact often arising in total variation based solutions. A convex cost function is given and an iterative algorithm is derived using majorization-minimization. The algorithm is both fast converging and computationally efficient due to the use of fast solvers for banded systems.
Download paper: GSTV_2013_ICASSP.pdf
Presentation slides: GSTV_2013_slides.pdf
Download Matlab software: GSTV_software (zip file)

Ivan W. Selesnick and Po-Yu Chen
Electrical and Computer Engineering
NYU Polytechnic School of Engineering
New York University
Brooklyn, New York
This material is based upon work supported by the National Science Foundation under Grant No. 1018020.
Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.