Filter delay demo

Illustratation of delay induced by an LTI system.

Contents

Start

clear
% close all

Define system

The system is defined by the difference equation

y(n) = 0.1 x(n) - 0.1 x(n-1) + 0.1 x(n-2) + 1.5 y(n-1) - 0.8 * y(n-2)

b = 0.1*[1 -1  1];

a = [1 -1.5 0.8];

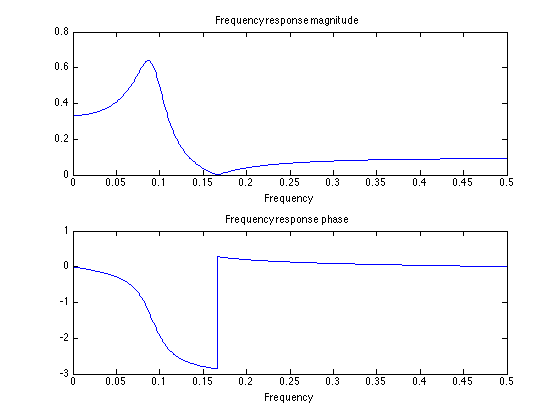
Plot frequency response

Use the 'freqz' function to calculate the frequency response.

[H, om] = freqz(b,a);
f = om / (2*pi);

figure(1)
clf

subplot(2, 1, 1)
plot(f, abs(H))
title('Frequency response magnitude')
xlabel('Frequency')

subplot(2, 1, 2)
plot(f, angle(H))
title('Frequency response phase')
xlabel('Frequency')

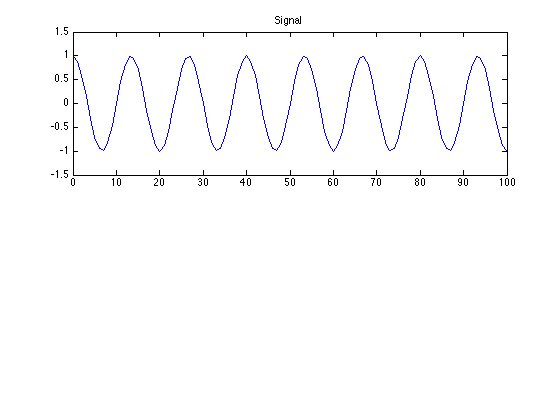
Create sinusoid

Create a sinusoid with a specified frequency

L = 100;
n = 0:L;

om1 = 0.15*pi;      % Frequency of sinusoid radians/sample
f1 = om1 / (2*pi);  % Frequency in cycles/sample

x = cos(om1*n);     % Cosine signal

figure(1)
clf
subplot(2,1,1)
plot(n, x)
title('Signal')
ylim([-1.5 1.5])

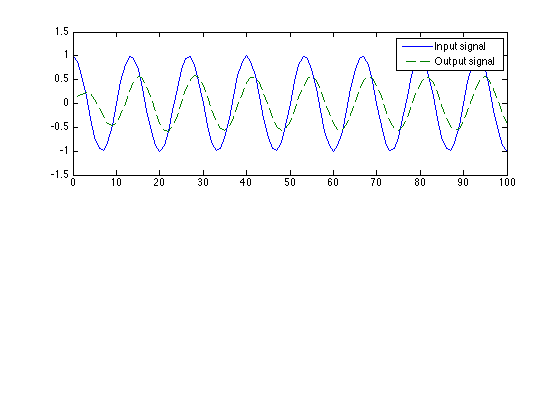
Output signal

Comput output signal. Plot input and output signals on the same plot. Notice the output signal is delayed with respect to the input signal. How many samples is the input signal delayed?

y = filter(b, a, x);    % Output signal

figure(1)
clf
subplot(2, 1, 1)
plot(n, x, n, y, '--')
legend('Input signal', 'Output signal')
ylim([-1.5 1.5])

Frequency response value at om1

The value H(om1) of the frequency response at om1 is a complex number.

I = sqrt(-1);
z1 = exp(I*om1);
d = length(b) - length(a);
H_om1 = 1/z1^d * polyval(b, z1) / polyval(a, z1)    % Value of frequency response at om1

H_om1 =

   0.4268 - 0.3733i

Magnitude at om1

H(om1)

A = abs(H_om1)

A =

    0.5670

Phase at om1

The angle of H(om1) will tell us the delay..

theta = angle(H_om1)

theta =

   -0.7186

Show magnitude and phase on frequency response plot

figure(1)
clf

subplot(2, 1, 1)
plot(f, abs(H), f1, A, 'o')
title('Frequency response magnitude')
xlabel('Frequency')

subplot(2, 1, 2)
plot(f, angle(H), f1, theta, 'o')
title('Frequency response phase')
xlabel('Frequency')

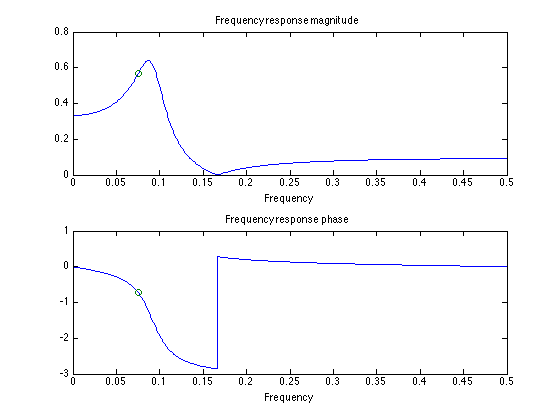
Delay (in samples) at om1

Compute the signal delay in samples

M = -angle(H_om1)/om1      % Delay in samples

fprintf('The delay is %.2f samples\n', M)

M =

    1.5250

The delay is 1.52 samples

Verify delay property

Plot the input and output signal together, where the input signal is delayed by M samples and multiplied by A. Observed that the output signal y(n) is in phase with the delayed input signal A x(n-M).

figure(1)
clf
subplot(2, 1, 1)
plot(n + M, A*x, n, y)
xlim([0 L])
legend('A x(n-M)', 'y(n)')
title( sprintf('A = %.2f, M = %.2f', A, M) )

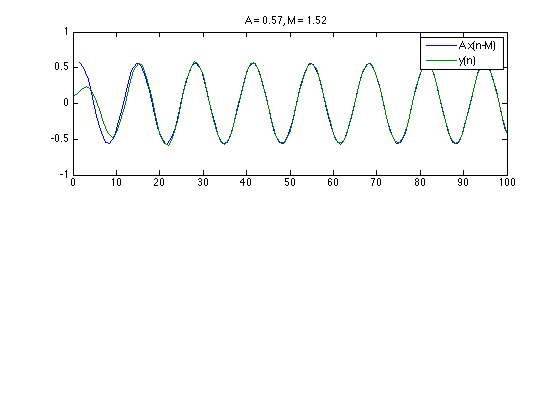
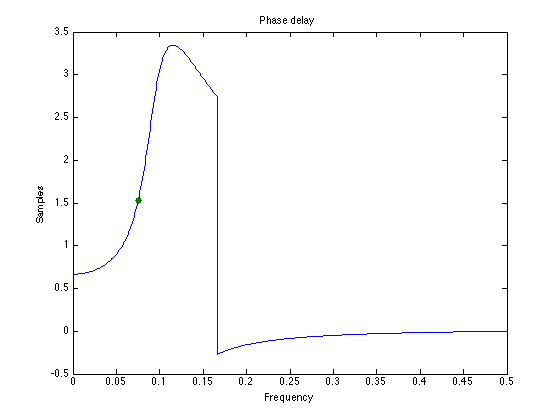
Plot phase delay function

Show delay M on plot of phase delay function.

figure(1)
clf
plot(f, -angle( H )./om, f1, M, '.', 'markersize', 20)
title('Phase delay')
ylabel('Samples')
xlabel('Frequency')

Published with MATLAB® R2013a